Neural Dynamic Modes
Computational Imaging of Dynamical Systems from Sparse Observations
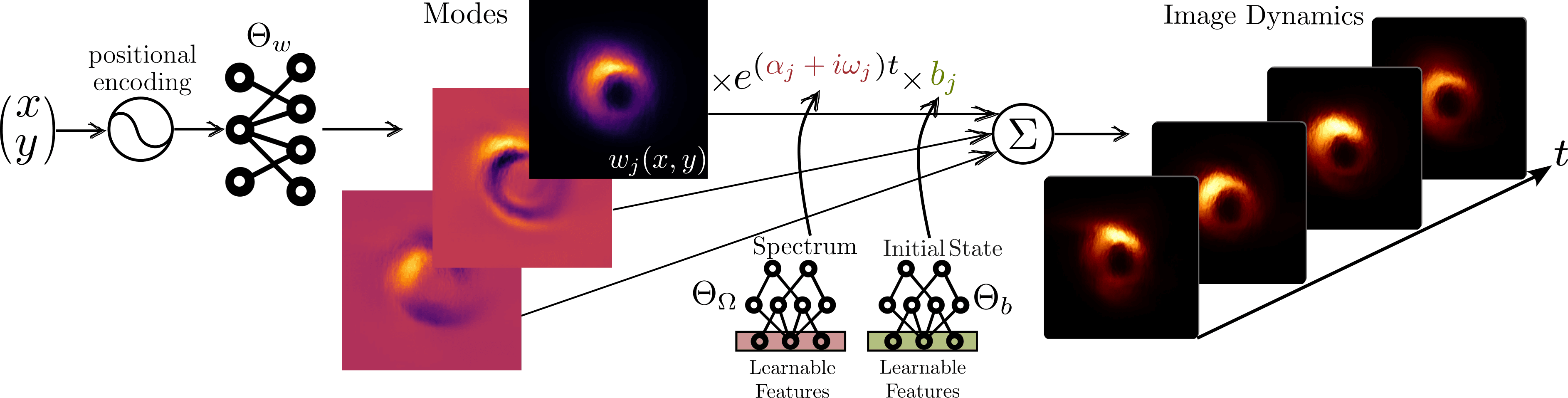
Abstract
Dynamical systems are ubiquitous within science and engineering, from turbulent flow across aircraft wings to structural variability of proteins. Although some systems are well understood and simulated, scientific imaging often confronts never-before-seen dynamics observed through indirect, noisy, and highly sparse measurements. We present NeuralDMD, a model-free framework that combines neural implicit representations with Dynamic Mode Decomposition (DMD) to reconstruct continuous spatio-temporal dynamics from such measurements. The expressiveness of neural representations lets the method capture complex spatial structures, while the linear dynamical modes of DMD introduce an inductive bias that guides training and supports stable, low-dimensional forecasting. We validate NeuralDMD on two challenging problems: recovering the evolution of plasma near the Galactic-center black hole, Sgr A*, and reconstructing near-surface wind-speed fields over North America from sparse station observations. In both cases NeuralDMD outperforms established baselines, demonstrating its potential as a general tool for imaging dynamical systems across astronomy, geoscience, and beyond.
Weather Data Assimilation
Our first set of experiments focuses on recovering full spatipo-temporal dynamics from sparse pixel observations. In this case, we use a simulated weather dataset, where the near-surface wind speed is observed at a limited number of locations. The goal is to reconstruct the full wind field from these sparse observations. NeuralDMD is trained on a sequence of wind fields, learning to capture the underlying dynamics and predict future states based on the sparse observations. The method demonstrates its ability to extrapolate and reconstruct the wind field, even when the observations are extremely sparse. Note, however, that the extrapolation capabilities of the current method, as it is formulated, is very limited; this is due to the inherent nonlinear dynamics of weather systems, which can lead to unpredictable behavior over longer time scales.
frame 0 / 1000
Reconstruction of near-surface wind-speed dynamics from extremely sparse pixel observations. In the extrapolation window, predictions deteriorate, which is indicative of the highly nonlinear nature of weather. However, NeuralDMD still captures the overall trend, predicting that the spiral structure of the wind will not continuously evolve, but rather will break down into smaller vortices. This is a common phenomenon in weather systems, where large-scale structures can become unstable and break apart into smaller features.
Black Hole Imaging
Our second set of experiments focuses on reconstructing the dynamics of the black hole Sgr A* from sparse Fourier measurements. The Event Horizon Telescope (EHT) captures images of black holes by observing their emissions at different radio frequencies, which are then combined to form a high-resolution image. However, these measurements are often sparse and noisy, making it challenging to reconstruct the full image. NeuralDMD is trained on these sparse and noisy observations, learning to capture the underlying dynamics and predict future states.
ngEHT Experiments
Ground Truth
NeuralDMD
Neural Representation
StarWarps
NeuralDMD is capable of reconstructing the black hole dynamics, and provide future predictions by modeling it as a linear dynamical system. We argue that the linear dynamical system well describes the black hole dynamics, especially at the resolution of the EHT. The following figure illustrates this point by showing the mean-squared reconstruction error of NeuralDMD for different blur levels. As the blur increases, NeuralDMD recovers the black hole evolution more accurately, demonstrating its robustness to noise and sparsity.
frame 0 / 1000
The figure plots the mean-squared reconstruction error of NeuralDMD for several blur levels. As the blur grows, NeuralDMD—by approximating the scene with linear dynamical modes—recovers the black-hole evolution ever more accurately. At 25 µas blur, the Event Horizon Telescope’s nominal resolution, the strongly nonlinear details are effectively smoothed away -- look at 1.27 hours (frame 290) for evidence of this phenomenon.
Robustness Studies
The following videos demonstrate performance of NeuralDMD as compared to neural representation and optDMD under varying levels of noise and sparsity. NeuralDMD consistently outperforms the other methods, demonstrating its ability to capture the underlying dynamics and provide accurate predictions.
Robustness Under Varying Noise Levels
Ground Truth
NeuralDMD
Neural Representation
optDMD
Robustness Under Varying Sparsity Levels
Ground Truth
NeuralDMD
Neural Representation
optDMD
Edge-on Simulations
The following test is more challenging than a face-on simulation, where the rotation dynamics of the accretion moves in and out of the image plane as the line of observation is almost parallel to the image plane. Whereas, in the face-on case (previous experiments), the majority of the dynamics is well-captured within the image plane.
Ground Truth
NeuralDMD
Neural Representation
Citation
@misc{saraertoosi2025neuraldynamicmodescomputational,
title = {Neural Dynamic Modes: Computational Imaging of Dynamical Systems from Sparse Observations},
author = {Ali SaraerToosi and Renbo Tu and Kamyar Azizzadenesheli and Aviad Levis},
year = {2025},
eprint = {2507.03094},
archivePrefix= {arXiv},
primaryClass = {cs.LG},
url = {https://arxiv.org/abs/2507.03094}
}Acknowledgements
We thank S. Nousias, A. Broderick, M. Shalaby, A. Fuentes, M. Foschi, S. Rashidi, R. Dahale, D. Posselt, and M. Als for helpful comments. A. L.’s work is supported by the Natural Sciences and Engineering Research Council of Canada (NSERC). This work was also supported by the Ontario Research Fund – Research Excellence under Project Number RE012-045.